十进制转二进制的方法 10进制转2进制算法介绍
时间:2018-01-31 来源:原版系统 - msdn我告诉你,msdn原版系统_个人软件测试
十进制转二进制的过程,说白点就是把人类算数的方式转换成机器语言(二进制),前者数据量巨大,后者只有0和1,占用很小,我们所熟悉的CPU便是使用二进制算法处理进程的,当然,二进制的使用可能较少,但我们有理由去了解。
十进制(以十为基础进位)数系的每一个位值有十个可能的值(0、1、2、3、4、5、6、7、8、9)。相反二进制(以二为基数进位)数系只有两个可能的值,即0和1。二进制系统是电子计算机的基本语言,真正的电脑程序员应了解如何将数字从十进制转换为二进制。
如果你是程序员,相信你已经足够了解转换方法了。
十进制转二进制的方法
方法一、余数短除法除以二

1、明确问题。举个例子,我们现在是要将一个十进制数字15610转换成二进制数字。先将这个十进制数作为被除数写在一个倒着的“长除法”的符号里。把目标数系的基数(在这里二进制是“2”)作为除数写在这个除法符号的外面。
用这个方法将计算过程可视化会更方便理解,因为整个计算过程只需将数字一直除以2。
为了防止转换前后发生混淆,建议将数系的基数写作每个数字的脚注形式。在本例中,十进制数字的脚注为10,二进制数字的脚注为2。

2、进行除法运算。把结果的整数部分(商数)写在长除法符号的下面,然后把它的余数(0 或 1)写在被除数的右边。
我们现在是以2为除数,因此得出的商为偶数,则余数为0;如果得出商为奇数,则余数记为1。

3、一直往下继续除,直到商为0为止。把每一个新的商数除以二,然后把余数写在被除数的右边。直到商数为0为止。

4、写出新的二进制数字。从最下面的余数开始,按顺序读到最上面。本例中,你会得到10011100。这就是十进制数字156的二进制形式。或者,我们可以以脚注等式的形式表达,即:15610 = 100111002
活用这个方法可以将所有十进制数字转换成任何进制表达。除数为2是因为我们最终想得到的以2为基数的数(即二进制数值) 。如果最终想得到其他数系的数字,用目标数系的基数代替这个方法里二进制的基数2 就可以了。例如,要得到基数为9的数,就用9来代替2作为除数 。最终的结果就是目标数系的数字表达。
方法二、降二次幂及减法混合运算

1、列表。将以2为底数的幂函数以表格形式从右到左列出来。从20开始,20为1。指数加一递增。列表直至函数值最接近需要计算的十进制数字为止。比如说,我们现在要将十进制数字15610转换为二进制。
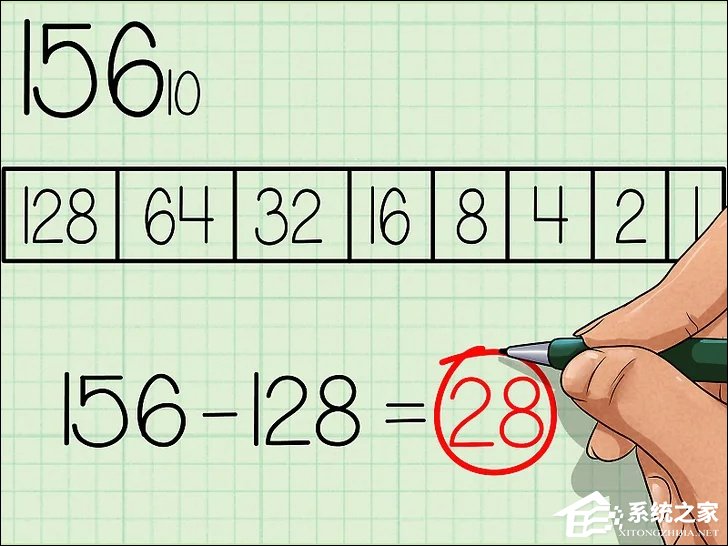
2、找出最合适的幂函数值。找出小于且最接近需计算数字的幂函数值。在本例中,128是小于156的、以2为底数的幂函数值中最大的数值。所以在二进制列表128的下方写上1。然后用156减去128,得出28。

3、继续计算。刚刚得出新得数28继续进行比较计算,看看哪一个幂函数值小于28。函数列表的下一个数字为64,64大于28,所以在64下方写上0。如此类推,看看那个数字小于28。
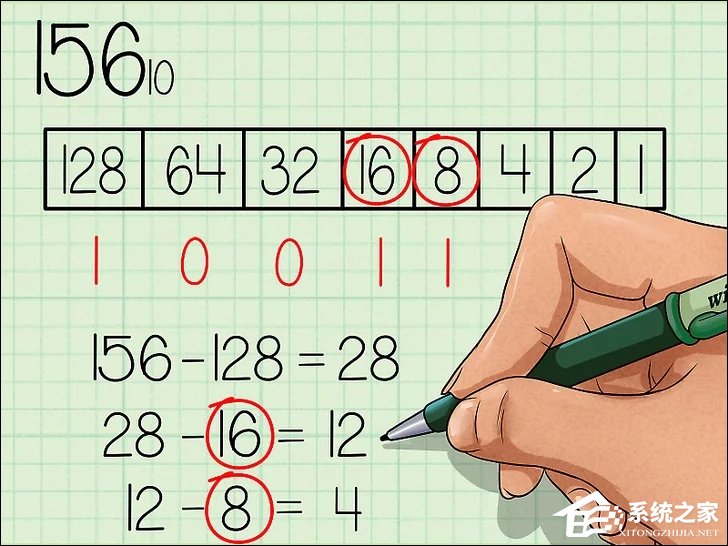
4、能减的数字记为1。本例中,64和48都不能被28减,得出正数。16可以被28减,得出12。8也能被12减,得出正数,所以在16和8下方都写上1。现在的差为4。

5、继续减法运算,直到列表的最后。记住在能被差减得出正数的数字下面记录为1,不能被减的数字下面记录为0。

6、写出二进制答案。得出的二进制数值就是列表下记录的数字排列。你应该能得出10011100。这就是十进制数字156的二进制表达。或者,我们可以以脚注等式的形式表达,即:15610 = 100111002
多次反复使用这个方法,你就能基本记住以2为底数的幂函数的值。就可以跳过第一步列表的步骤了。
小提示:
● 操作系统里安装好的计算器也可以用作十进制和二进制之间的转换,但作为一个程序员,能清楚地了解这个转换的原理会更好,点击“查看” 然后选择 “程序员”就可以看到转换器了。
● 反过来转换,从二进制转换为十进制通常更容易入门。
● 多练习,试着转换十进制数 17810,6310,和 810。你会分别得到以下二进制答案 :101100102,1111112,和10002. 试着转换20910,2510,和 24110,会得出110100012,110012,和111100012.
以上内容便是十进制转二进制的方法介绍,二进制虽然是当下计算机流行的一种架构,但计算机并不仅仅只有二进制,还有三进制算法,这是后话……
相关信息
-
-
2019/05/07
笔记本键盘灯不亮,详细教您笔记本键盘灯怎么打开 -
2018/08/04
芝麻信用可以用来干嘛? -
2018/07/23
Win10打开文件提示没有与之关联的程序的解决方法
-
-
无线网卡切换为AP模式时提示ICS启动失败的解决方法
无线网卡切换为AP模式时提示ICS启动失败怎么办?当我们在使用计算机的时候,时常会出现各种问题,有时候会出现系统提示无线网卡切换为AP模式时提示ICS启动失败的情况,这是什么原因...
2018/07/23
-
Win10打开文件提示没有与之关联的程序的解决方法
Win10打开文件提示没有与之关联的程序怎么办?有些Win10用户们在打开文件的时候,系统突然弹出“该文件没有与之关联的程序来执行该操作。请安装一个程序,或者,如果已安装程序,请在...
2018/07/23
系统教程栏目
栏目热门教程
人气教程排行
- 1 安装系统时会出现蓝屏或死机怎么办?
- 2 Win10系统怎么安装iso镜像文件 Win10系统安装iso镜像文件方法
- 3 Win10系统无法正常运行经典游戏的解决方法
- 4 惠普笔记本原装Win8重装成Win7系统的教程
- 5 固态硬盘是什么东西?固态硬盘内部结构详解
- 6 Win10开始菜单无法打开怎么解决 Win10开始菜单无法打开解决方法
- 7 微信朋友圈怎么发布心形九宫图 微信朋友圈发布心形九宫图方法
- 8 酷睿i3和i5的区别是什么?电脑处理器i3和i5的区别介绍
- 9 WinXP如何去掉桌面图标的蓝色阴影?
- 10 装系统提示Output error file to the following location A:\ghosterr.txt怎么办?
站长推荐
热门系统下载
- 1 Windows 7 SP1 简体中文 旗舰版 64位 官方原版系统ISO
- 2 Windows 7 SP1 简体中文 专业版 64位 官方原版系统ISO
- 3 Windows 7 SP1 简体中文 旗舰版 32位 官方原版系统ISO
- 4 Windows10 21H1 19043 简体中文 64位/32位 官方原版系统ISO
- 5 Windows10 22H2 19045 简体中文 64位 官方原版系统ISO
- 6 Windows10 1909 简体中文 64位/32位 官方原版系统ISO
- 7 Windows 8.1 简体中文 专业版 64位 官方原版系统ISO
- 8 Windows11 简体中文 22H2 22621 64位 官方正式版系统ISO
- 9 Windows10 2009 20H2 正式版 64位/32位 官方原版系统ISO
- 10 Windows10 2004 20H1 64位/32位 官方原版系统ISO